- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
CST2013: Which Mesh to Use
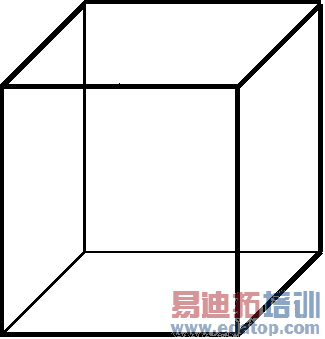
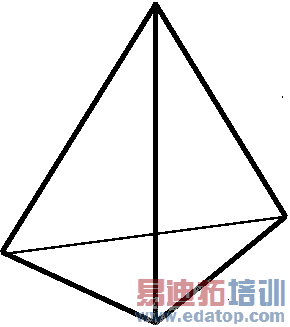
For the spatial discretization the Finite Integration Method (FI-Method) is used. The method requires the computational domain to be covered by a mesh. Two different mesh types are available: hexahedral and tetrahedral meshes. In the figure below a single element for each mesh type is displayed.
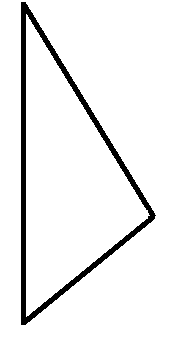
For the Integral Equation solver a surface mesh will be created.
|
|
|
hexahedron | tetrahedron | surface |
Setting the mesh type
You select the mesh type for your computation in the respective solver dialog. Please note that almost all CST solvers work with a hexahedral mesh, while only some solvers provide a tetrahedral or surface mesh method.
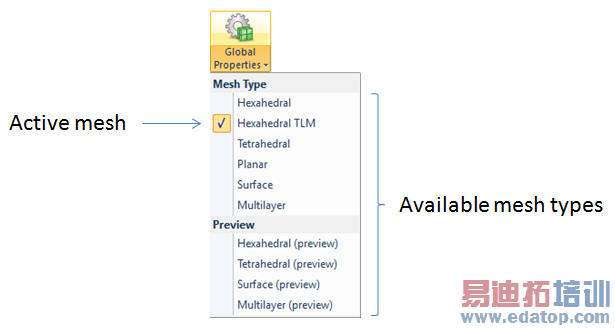
Another way to select the mesh type is by using the menu available with Home: Mesh Global Properties
Global Properties  . However, this is just for previewing the mesh. A change of the solver method will change the active mesh type.
. However, this is just for previewing the mesh. A change of the solver method will change the active mesh type.
Differences between CST surface, hexahedral and tetrahedral meshes.
CST hexahedral meshes:
In general, hexahedral meshes do not conform to material jumps; please note that this is not necessary because CST provides the Perfect Boundary Approximation? (PBA) and the Thin Sheet Technology (TST) in combination with hexahedral meshes.
If the CST Multilevel Subgridding Scheme (MSS) is used, refinement can be local with respect to all coordinate directions. Otherwise, refinement can be local with respect to one coordinate direction, i.e. in order to account for details of the model whole mesh planes will be inserted.
Hexahedral meshing is very robust even for most complex imported geometries.
Hexahedral meshes without MSS? are highly structured and lead to very fast computations.
In contrast, CST tetrahedral and surface meshes
are conform to solid-boundaries and consequently conform to material jumps.
The mesh refinement can be local with respect to all coordinate directions, i.e. single elements can be refined.
Surface meshing leads to a smaller number of unknowns.
Which mesh type is most appropriate for a given simulation task?
It is difficult to provide a general statement on how to decide which mesh type should be applied for a given problem. However, as a rule of thumb, using CST hexahedral meshes (without MSS?) will often lead to faster computations because the solver can take advantage of their additional structure. Moreover, hexahedral meshing is very robust concerning complex geometries. This may be important if you must deal with imported structures.
However, if your problem setting includes strongly local details in the geometry or solution, structured hexahedral meshes may produce a large overhead in the number of elements for the part of the computational domain that does not need a fine mesh. For these types of problems, tetrahedral meshes or hexahedral meshes with MSS? are more suitable because they offer more flexibility.
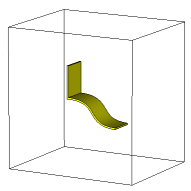
| A typical example of when the application of a tetrahedral mesh or the application of MSS? may be recommended is the presence of small, curved gaps or thin, curved dielectric solids. In these cases, a sufficiently fine structured hexahedral mesh may include many mesh cells, whereas a tetrahedral mesh or a hexahedral mesh using MSS? can resolve the gap or thin-curved solid locally (see the pictures below). Hence, using a tetrahedral mesh or hexahedral mesh combined with MSS? may lead to a smaller number of unknowns for such situations. One must decide between flexibility or higher speed for more unknowns. Clearly, some experience is necessary to know which mesh type fits best for a given problem. Below are given the different mesh types for the geometry on the left. |
Using standard hexahedral meshing for this example (without MSS?), the mesh refinement is not restricted to the fine geometry. |
Using the Multilevel Subgridding Scheme? more flexibility is available - small mesh cells are concentrated near the fine geometry. |
Tetrahedral meshing is even more flexible, small mesh cells appear only in the surrounding of the small scale geometry and are conform to the model geometry. |
Surface meshing is as flexible as the tetrahedral meshing. The meshing is reduced to the object boundaries. |
Verification by comparison
You can get crucial benefit by the use of all, a surface, a tetrahedral and a hexahedral mesh for the same problem: The results can be compared. This yields an additional validity check for your numerical results.
Note that this is not a time-consuming task. In contrast to the use of different software tools for validation you can use different solver methods in the same CST software without setting up your computational model again!
CST微波工作室培训课程套装,专家讲解,视频教学,帮助您快速学习掌握CST设计应用
上一篇:CST2013: List of Fixpoints
下一篇:CST2013: Add Absolute Fixpoint
 最全面、最专业的CST微波工作室视频培训课程,可以帮助您从零开始,全面系统学习CST的设计应用【More..】
最全面、最专业的CST微波工作室视频培训课程,可以帮助您从零开始,全面系统学习CST的设计应用【More..】
频道总排行
- CST2013: Mesh Problem Handling
- CST2013: Field Source Overview
- CST2013: Discrete Port Overview
- CST2013: Sources and Boundary C
- CST2013: Multipin Port Overview
- CST2013: Farfield Overview
- CST2013: Waveguide Port
- CST2013: Frequency Domain Solver
- CST2013: Import ODB++ Files
- CST2013: Settings for Floquet B